BAB 2
SISTEM PERTIDAKSAMAAN DUA VARIABEL
(LINEAR-KUADRAT DAN KUADRAT-KUADRAT)

Bentuk Umum SPtLDV (Sistem Pertidaksamaan Kuadrat Dua Variabel)
Bentuk umu dari sistem pertidaksamaan linear dua variabel adalah suatu kalimat terbuka dari ilmu matematika yang didalamnya berisi dua variabel. Dengan masing-masing dari variabel berderajat satu dan dihubungkan dengan tanda ketidaksamaan. Tanda ketidaksamaan yang dimaksud ialah: >, <, ≤, dan ≥.
Maka dapat disimpulkan bentuk dari pertidaksamaan linear dapat dituliskan sebagai berikut:
♦ Bentuk Pertidaksamaan
♦ Contoh kalimat dari pertidaksamaan
|
Beberapa contoh kalimat diatas merupakan kalimat terbuka yang menggunakan tanda hubung seperti: >, <, ≤, dan ≥. Hal ini menjadi suatu tanda bahwa kalimat tersebut merupakan kalimat pertidaksamaan.
Himpunan Penyelesaian SPtLDV

Dalam menyelesaikan pertidaksamaan linear kuadrat dua variabel ada beberapa hal yang harus anda kuasai, yang kesemuanya itu bertujuan untuk mempermudah anda dalam mengerjakannya.Penyelesaian suatu pertidaksamaan linear dua variabel adalah pasangan ber urut (x,y) yang dapat memenuhi pertidaksamaan linear tersebut.
Perlu anda ketahui juga bahwa himpunan dari penyelesaian tersebut dapat dinyatakan degan sebuah daerah pada bilangan kartesius (bidang XOY) yang ditandai dengan adanya arsiran.
Agar lebih paham mengenai daerah himpunan dari penyelesaian pertidaksamaan linear dua peubah. berikut contoh dan penjelasannya.
Contoh Penjelasan Soal
3x + 4y ≤12
Jawab:
- Langkah pertama yang harus anda kerjakan adalah melukis garis 3x + 4y = 12 dengan cara menghubungkan titik potong garis yang ada dengan sumbu X dan Sumbu Y.
- Titik Potong garis yang ada pada sumbu X memiliki arti sebagai Y = 0, dan didapatkan x = 4. Dengan menggunakan ketentuan menjadi (4,0)
- Lalu tarik titik potong garis dengan sumbu Y artinya jika X = 0, maka akan didapat hasil Y = 3. Dengan ketentuan menjadi (0,3)
- Garis 3x + 4y = 12 bilangan ini yang nantinya akan membagi bidang kartesius menjadi dua bagian.
- Untuk menentukan daerah mana sih yang nantinya akan di arsir untuk menentukan daerah himpunan penyelesaian? Maka akan dilakukan salah satu titik uji dari salah satu titik yang ada pada kartesius tersebut daerah lain.
Sebagai contoh disini kita mengambil titik daerah lainnya yaitu (0,0) agar mempermudah anda dalam pengerjaannya. Lalu dengan titik (0,0) tersebut akan diperoleh bilangan seperti ini:
3x + 4y ≤12
= 3 (0) + 4 (0) ≤ 12
= 0 + 0 ≤ 12
= 0 ≤ 12 ( Nol kurang dari sama dengan dua belas)
Sehingga diperoleh 0≤12 benar, yang berarti sangat memenuhi sebagai daerah penyelesaian (DP).
Mencari nilai x dan y dari tabel
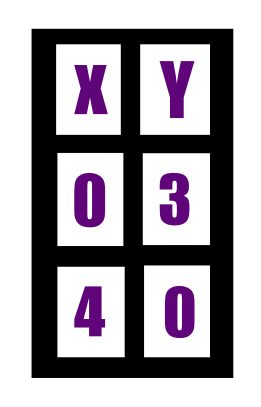
Dari gambar diatas dapat diketahui bahwa untuk nilai x = (4,0) dan untuk nilai y = (0,3).
Jadi daerah penyelesaiannya yaitu daerah yang masuk dalam titik (0,0). yakni daerah yang di arsir pada gambar berikut ini.
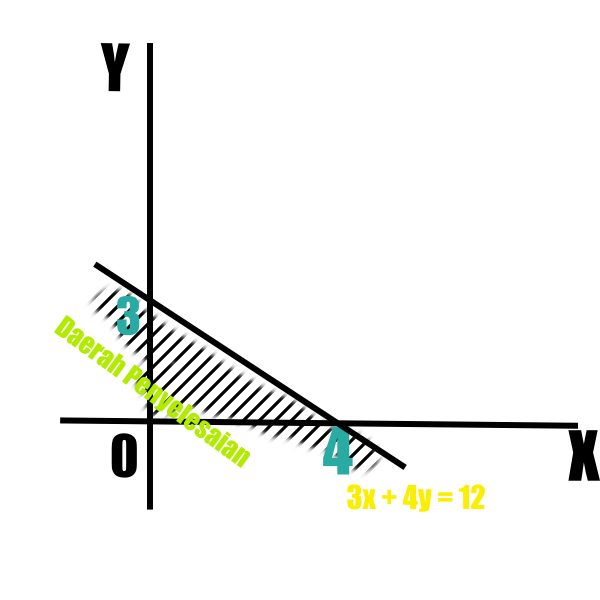
Daerah Penyelesaian Pertidaksamaan
Himpunan penyelesaian sistem pertidaksamaan linear dua variabel (SPtLDV) adalah himpunan titik-titik pasangan berurut (x,y) dalam suatu bidang yang bernama kartesius yang nantinya dapat memenuhi seluruh pertidaksamaanlinear pada sistem tersebut. Sehingga daerah himpunan penyelesaiannya merupakan irisan dari beebrapa himpunan penyelesaian yang ada dari suatu pertidaksamaan dalam SPtLDV.
Agar lebih paham mengenai daerah penyelesaian pertidaksamaan, berikut ini ada satu contoh yang akan diberikan untuk anda. Simak baik-baik ya!
Contoh Soal Pembahasan
2x + 3y ≤ 12 (Pilih titik (0,0) untuk mendistribusikan kedalam pertidaksamaan)
Nilai y
2x + 3y = 12
2 (0) + 3y = 12
3y = 12
y = 4
Nilai x
2x + 3y = 12
2x + 3(0) = 12
2x = 12
x = 6
Contoh Mencari Nilai X dan Y menggunakan Tabel
Maka dapat dituliskan dalam tabel sebagai berikut

Dari gambar diatas dapat ditarik kesimpulan bahwa nilai x = (6,0) sedangkan nilai untuk y = (0,4).
Daerah penyelesaiannya dapat digambarkan seperti berikut ini
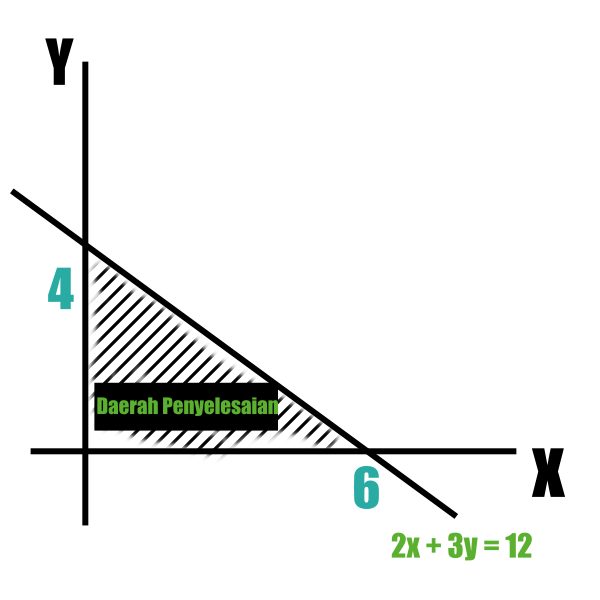
Dari kartesius diatas dapat ditarik kesimpulan bahwa nilai 2x + 3y ≤ 12 menyatakan benar bahwa bilangan tersebut memenuhi pertidaksamaan. Nilai untuk garis x yaitu (6,0) dan y yaitu (0,4) sehingga dapat ditarik garis seperti gambar diatas. Dan bagian yang diarsir ialah sutu tanda pembuktian dimana itu adalah penyelesaian dari pertidaksamaan kuadrat.



Tidak ada komentar:
Posting Komentar