BAB 10
GETARAN HARMONIS

Pengertian Getaran Harmonik
Gerak harmonik merupakan gerak sebuah benda dimana grafik posisi partikel sebagai fungsi waktu berupa sinus (bisa dinyatakan dalam bentuk sinus atau kosinus). Gerak semacam ini disebut dengan gerak osilasi atau getaran harmonik.
Contoh getaran harmonik
- dawai pada alat musik
- gelombang radio
- arus listrik AC
- denyut jantung.
- Galileo di duga sudah memakai denyut jantungnya untuk pengukuran waktu dalam pengamatan gerak.
Syarat Getaran Harmonik
Syarat suatu gerak dikatakan getaran harmonik, yaitu antara lain :
- Gerakannya periodik (bolak-balik).
- Gerakannya selalu melewati posisi keseimbangan.
- Percepatan atau gaya yang bekerja pada benda sebanding dengan posisi/simpangan benda.
- Arah percepatan atau gaya yang bekerja pada suatu benda selalu mengarah ke posisi keseimbangan.
Periode dan Frekuensi Getaran Harmonik
a. Periode dan Frekuensi Sistem Pegas
Pada dasarnya, gerak harmonik adalah suatu gerak melingkar beraturan pada salah satu sumbu utama. Oleh sebab itu, periode dan frekuensi pada pegas bisa dihitung dengan menyamakan antara gaya pemulih (F = -kX) dan gaya sentripetal (F = -4π 2 mf2X).
Periode dan frekuensi sebuah sistem beban pegas hanya bergantung pada massa dan konstanta gaya pegas.
b. Periode dan Frekuensi Bandul Sederhana
Sebuah bandul sederhana terdiri atas sebuah beban bermassa m yang digantung di ujung tali ringan (massanya dapat diabaikan) yang panjangnya l. Bila beban ditarik ke satu sisi dan dilepaskan, maka beban berayun melalui titik keseimbangan menuju ke sisi yang lain.
Bila amplitudo ayunan kecil, maka bandul melakukan getaran harmonik. Periode dan frekuensi getaran pada bandul sederhana sama seperti pada pegas. Artinya, periode dan frekuensinya dapat dihitung dengan menyamakan gaya pemulih dan gaya sentripetal.
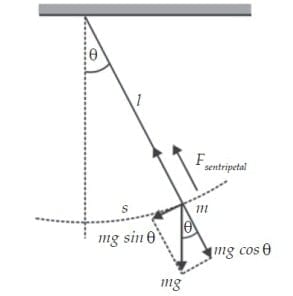
Persamaan gaya pemulih pada bandul sederhana adalah F = -mg sinθ . Untuk sudut θ kecil (θ dalam satuan radian), maka sin θ = θ . Oleh karena itu persamaannya dapat ditulis F = -mg (X/l). Karena persamaan gaya sentripetal adalah F = -4π 2 mf2X, maka kita peroleh persamaan sebagai berikut.
Periode dan frekuensi bandul sederhana tidak bergantung pada massa dan simpangan bandul, tetapi hanya bergantung pada panjang tali dan percepatan gravitasi setempat.

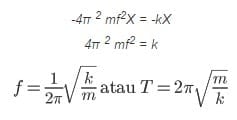
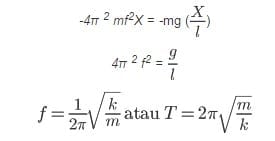


Tidak ada komentar:
Posting Komentar